Circle of Fifths

Fun with the Circle Of 5ths and Identifying Chords

In the process of teaching myself music theory, I have become very impressed with the power of the Circle of 5ths (here I am talking about the standard circle in 12-equal temperament). I have cataloged some interesting properties, and I am always on the lookout for more.

1. A line through the center identifies notes which are a tri-tone apart, and the line slices the circle into 2 keys, which are named by moving one step clockwise from the line (the end points are in both keys). This also sheds light on how keys are related to each other, by being close or far apart around the circle. If they are close, then they share a lot of notes.
   

---

2. There is no need to write on the diagram where the relative minor keys are, or draw a separate diagram for minor keys, because they can easily be found (more on this later):
   

---

3. The pattern of the chromatic scale (notes most closely related in pitch) is obtained by drawing a line through the center, say d^# to a, and then looking counter-clockwise (descending through the chain of 5ths) to find the note below d^#, and clockwise (ascending a 5th) to the note above d^#. The pattern of the diatonic scale is obtained by slicing the circle to isolate the particular key like before, and then hopping around the half circle by 2 steps each time, never straying to the other side of the tri-tone line.
   

---

4. Likewise, if you can only remember part of the circle and you want to construct the rest, you need only draw a line through the center from the note that you remember, and you can locate its sharp (by going clockwise one step) or its flat (by going counter-clockwise):
   

---

5. Chord Resolution
   
   It is easy to remember what dominant 7th chord resolves to what tonic chord (major or minor) by going counter-clockwise around the circle of 5ths.
   

---

6. Symmetries
   
   The circle and the positions of the dots are invariant under the following operations:
   • 12 clockwise rotations and 12 counter-clockwise rotations (rotate c to g, c to d, etc...) But rotating clockwise by n/12 of a full turn has the same result as rotating (12-n)/12 counterclockwise, so there are only 12 distinct rotations in all, not 24.
   • There are 12 lines through the center for reflections (axes of symmetry). 6 are lines through pairs of notes (tri-tones) and 6 are through the mid points between notes.
   • There is one reflection through the center point, but it is equivalent to a rotation of 180 degrees, so we won't discuss this one further.

---



7. Rotating an interval line or a chord shape corresponds to transposing to a different key. Here we rotate the C major triad shape 4 positions clockwise to get E major:
8. If we anticipate a little the chord diagrams that occur later on this page, it is even possible to determine what are the chords within a given key. In the key of C major, we can fit in the shape for the F major triad, we shift it once clockwise and get the C major and then the G major. When we try to shift it again, the 3rd hits the tri-tone line and has nowhere else to go but up to the note f giving us D minor now. Continuing to shift, we get Am and Em. Then we hit the tri-tone line again, and this time the chord shape is deformed into B-diminished. The main idea is that you can determine the chords by what chord shape will fit. If I would have realized this earlier, maybe I wouldn't have had to make these chord charts !
   

---

9. Intervals
   
   • If we regard c as the lowest note in the octave, we see the right half of the circle is comprised of major intervals (capital M) and the left side is composed of the complementary minor intervals (baby m). Complementary means that the number of semi-tones of a segment and its mirror image always adds to 12. And of course we can rotate this arrangement of arrows to eminate from any other note on the circle, which is what is really important. (Thanks to Jamie Alamo for a correction to this).
     
   
   
   
   • If we now let the left half circle be notes in the octave below c and the right half be notes above, we get mirror images of exclusively major intervals.
     
     
   • We can play the same game by letting the right side of the circle be in the octave below c and the left side above and get mirror images of minor intervals, but since it is late at night I won't draw that.

---

10. Reflections
    Reflections are very cool because they always have the property of turning major triads into minor ones and vice versa! First observe the symmetry between C and C_m:
    
    
    • We can reflect through any symmetry line; the rule is that the 5th of the major triad is interchanged with the root of the minor triad . Thus we can easily find the name of any of these reflected chords.
    • This implies an equal importance of major and minor triads. See Theory of Chords page.
    • Not only is the root triad reflected, but the entire key is reflected. In the picture you can check that all the notes of C major are mapped to the notes of C (natural) minor.
    • As an example, consider reflecting the C major triad through the line joining a^b to d. The note g is mapped to a which means that C is mapped to A_m (NOTE: this reflection is not what is in the picture above or the table shown below). The tri-tone line of C is b-f and that is the perpendicular bisector of the a^b to d line. All the notes in the key of C are preserved, but C is interchanged with A_m. This perhaps sheds some light on why A_m. is called the relative minor to C!

    Reflection between C major and C minor (the parallel minor)

    Roman number	Notes	Chord name	Chord name	Notes	Roman number
    I	c-e-g	C	Cm	g-eb-c	i
    ii	d-f-a	Dm	Bb	f-b-d	VII
    iii	e-g-b	Em	Ab	eb-c-ab	VI
    IV	f-a-c	F	Gm	d-bb-g	v
    V	g-b-d	G	Fm	c-ab-f	iv
    vi	a-c-e	Am	Eb	bb-g-eb	III
    viio	b-d-f	B dim	D dim	ab-f-d	iio

    Why does any major triad always reflect to a minor triad? It is enough to show this for C major, since we can rotate to any other major chord. From the root note c, the 5th is 1 step clockwise (we always measure distances clockwise, so from now on I'll just say the distance is "+1 steps") and the major 3rd is +4 steps and the minor 3rd is -3 steps. From rotational symmetry, this is true for all the chords.

    Now we make an arbitrary reflection of the circle, and so c is mapped to c', and likewise e → e', and g → g'. We have to show that this new triad is a minor chord. c' and g' are still adjacent to each other, since reflections can't change distances, but now g' is -1 steps from c', so g' is the root and c' is the 5th. Since in fact all intervals are reversed in reflections (we'll prove this at the end), the distance from c to e is +4 and thus the distance from c' to e' is -4. This means that the distance from g' to e' is -3 and we have all the intervals for a minor chord.

    Lemma: In any reflection, the direction of any interval is reversed.

    If a point x on the circle is counter clockwise from a point y then the distance (measured clockwise) satisfies d(p,x) < d(p,y) for any p on circle. Let L be an arbitrary line of reflection and p any one of the 2 points when L meets the circle (just choose one and forget the other). A reflection through L is the same thing as taking a point x that is +n units from p and sending it to z' which is -n units from p. Thus under a reflection, if d(p,x) = n and d(p,y) = m with n < m, we get d(p,x') = -n and d(p,y') = -m and obviously -n > -m so the interval is reversed. ♠

[Some of above interesting properties where suggested to me by Dr. Matt Fields on Dec 26, 2003 in the rec.music.theory usenet group].

---

11. Resolution of the tri-tone
    In the Key of C, the tri-tone line seems to contract (and flip endpoints) to go to c-e. But from the symmetry of the circle of 5ths, this same tri-tone could contract to f^#-a^# in the Key of F^#.
    Observe how this is different on the spiral of 5ths .
    
    

    ---

Identifying Chords

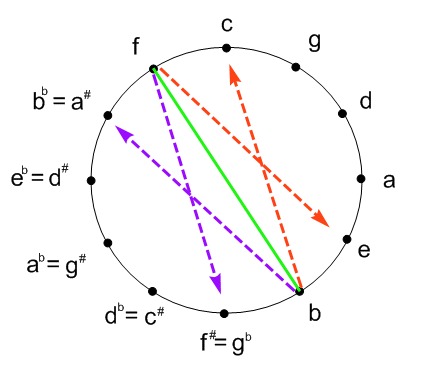
Here symmetry plays a big role also. We have already remarked on the symmetry between major and minor chords. Here we observe that symmetry within a chord makes it ambiguous as to what key it belongs to.

1. Here is the characteristic pattern of steps around the circle, always going clockwise, for the major and minor chords:
   

---

2. Here we have the Diminished and Augmented C chords. Note the lines of symmetry in each. Then look at these chords in their more natural habitat outside 12-equal. These chords are a stack of 3rds.
   

---

3. The suspended chords:
   Note how C-sus symmetrically contains the note c's two nearest neighbors and when we hear the chord C-sus, it wants to resolve to C major. These chords are a stack of 5ths.
   

---

4. The 6th chords:
   Note that C6 can be thought of as the C major triad unioned with Am. Also note that if we reflect C6 through the line between c and g (like we did for C to Cm) we don't get Cm6 (we get Cm7!) This is puzzling... C6 is a rotation of 2 steps clockwise of Cm7, so C6 could also be named Am7.

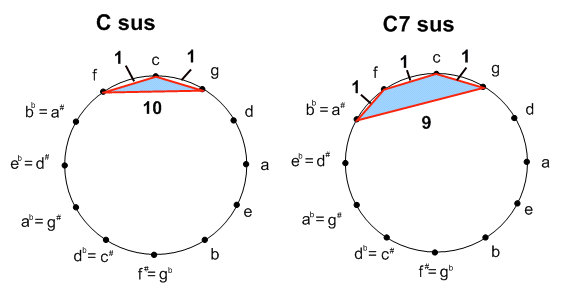
   Cm6 is an "inverse" of the resolvent C7_F (swap the 2 and 3 length segments, not the tri-tone line).
   

---

5. The 7th chords:
   Note that Cmaj7 does not reflect to Cm7, but recall C6 does! The chord that Cmaj7 does reflect to is a rotation of 4 steps counter-clockwise of the original, namely A^bmaj7. Cm7 could equally well be named E^b6.
   

---

6. The dominant 7th chord, which has the classic resolution to F (major or minor). A rule of thumb for identifying the root chord for which it resolves is the mid-point of the segment of length 2; the end point notes are the 4th and 5th of the tonic. Note that its longest segment is the tri-tone line, which separates the key of F!

   Also exhibited here is C diminished 6th, which is extremely symmetrical, and therefore, key ambiguous (we could just as easily name it as A dim 6, F^# dim 6 or E^b dim 6). It can be thought of as Cdim + F^#dim or E^bdim + A dim. It is very interesting to look at it outside 12-equal where it loses its symmetry!
   

---

7. The 9th chords:
   C9 is C major simultaneous with G minor.
   Cm9 is C minor simultaneous with G minor.
   

I got the idea for drawing chords in the circle of fifths from Harmony and Ear Training at the Keyboard by Stanley N. Shumway. In Appendix 1 Symmetrical Sonorities he features many different diagrams than found here such as modes, whole tone scales, etc. (and many diagrams found here are not in Shumway's text).

Musical-U is a company that has an interesting discussion of How To Use The Circle Of Fifths . They also present many other topics related to music and have study courses available.