Theory of Temperament and Meantone

Jeff Jensen Feb 2005

Contents

Introduction

Temperament is the art of cleverly compromising between competing, and mutually exclusive, acoustical and musical goals. I have struggled for a long time to understand meantone temperaments, why exactly certain keys should be unplayable, and what does it mean when people say things like "¼-comma meantone is the same thing as 31-equal temperament", or if that is even true. The following represents my best attempt to make sense of it all, with what I believe are some novel diagrams and mathematical expressions [but if anything is original here, there is also a good chance that it is a mistake, so I would appreciate any corrections!].

I try to draw as many pictures and give as many tables as possible. The focus is on physics, not number theory, so there is a lot of talk about harmonics and iterative calculation by computer replaces a discussion of continued fractions. By going a different route, you see different scenery! You could generate the Pythagorean scale fractions from (3/2)ⁿ with octave equivalence rescaling by powers of 2, but I find it more pedantically sound to work with 3ⁿ with rescaling 2, since that brings out sharply that it is the 3rd harmonic underneath it all. I don't want to give a cookbook of the various values in cents of the notes in a bunch of different tunings, which is very well done in many places, most notable J.M. Barbour's Tuning and Temperament. I want to understand the general principles behind them. But don't worry; there is nothing here more advanced than high school algebra.

This discussion is based in a large part on Mathematics and Music by Dave Benson Specifically, portions of chapter 5 and 6 and Appendicies E and J. Indeed, the presentation I give grew out of attempting to understand Benson's material, and could be considered a reworking and extension of what he has.

I would like to thank Manuel Op de Coul and Pierre Lewis for reading this and pointing out certain specific errors to me; any remaining ones I am responsible for.

A Chain of Perfect 3rd Harmonics (Pythagorean scales)

Largely of historical interest today (although it is still played by proponents of early music) the Pythagorean scale is, for us, a theoretical springboard; the simplest case which illustrates all the others. The following diagram is usually called the Spiral of 5ths. "5th" refers to adjacent notes in the spiral being 5 notes in a diatonic scale apart: g is 5 scale steps up from c, which is 5 steps up from f and so on. I think it is much clearer to observe that what is really going on is that the pitch of g is the pitch of the 3rd harmonic of c, rescaled by an apporpriate factor of 2 (in this case 1/2) so that all the notes lie in the same octave. This holds for all the other notes as well. Below I will give explicit formulas for calculating these values.

The spiral is to emphasize that notes that are equal in pitch (enharmonic) in the standard 12-equal temperament are not equal here ( thus g^## is not quite the same pitch as a, which in turn is not the same pitch as b^bb).

Fig. 1

The Pythagorean generating function is, for an integer n:
P_y(n) = 3ⁿ 2^{κ(n; 3)}
where κ(n; 3) is the unique integer in the interval [ n log(3)/log(2) - 1, n log(3)/log(2) ]
Thus 2^{κ(n; 3)} is the octave rescaling factor. You can see it depends also on the parameter 3 (the 3rd harmonic); this will be modified when we discuss meantone temperament below.

Here is a table I have calculated of the values of the Pythagorean function P_y(n), which I have found frequently useful for reference purposes. You can see how the power of 2 does not vary in any clean, simple way with the power of 3. (The source code to generate this table as large as you like is available at the end of this document).

Table 1: Pythagorean fractions
Index Three Two Fractional Value Note Name

20 3²⁰ 2^-31 3486784401 / 2147483648 F^###

19 3¹⁹ 2^-30 1162261467 / 1073741824 B^##

18 3¹⁸ 2^-28 387420489 / 268435456 E^##

17 3¹⁷ 2^-26 129140163 / 67108864 A^##

16 3¹⁶ 2^-25 43046721 / 33554432 D^##

15 3¹⁵ 2^-23 14348907 / 8388608 G^##

14 3¹⁴ 2^-22 4782969 / 4194304 C^##

13 3¹³ 2^-20 1594323 / 1048576 F^##

12 3¹² 2^-19 531441 / 524288 B^#

11 3¹¹ 2^-17 177147 / 131072 E^#

10 3¹⁰ 2^-15 59049 / 32768 A^#

9 3⁹ 2^-14 19683 / 16384 D^#

8 3⁸ 2^-12 6561 / 4096 G^#

7 3⁷ 2^-11 2187 / 2048 C^#

6 3⁶ 2^-9 729 / 512 F^#

5 3⁵ 2^-7 243 / 128 B

4 3⁴ 2^-6 81 / 64 E

3 3³ 2^-4 27 / 16 A

2 3² 2^-3 9 / 8 D

1 3¹ 2^-1 3 / 2 G

0 3⁰ 2⁰ 1 C

-1 3^-1 2² 4 / 3 F

-2 3^-2 2⁴ 16 / 9 B^b

-3 3^-3 2⁵ 32 / 27 E^b

-4 3^-4 2⁷ 128 / 81 A^b

-5 3^-5 2⁸ 256 / 243 D^b

-6 3^-6 2¹⁰ 1024 / 729 G^b

-7 3^-7 2¹² 4096 / 2187 C^b

-8 3^-8 2¹³ 8192 / 6561 F^b

-9 3^-9 2¹⁵ 32768 / 19683 B^bb

-10 3^-10 2¹⁶ 65536 / 59049 E^bb

-11 3^-11 2¹⁸ 262144 / 177147 A^bb

-12 3^-12 2²⁰ 1048576 / 531441 D^bb

-13 3^-13 2²¹ 2097152 / 1594323 G^bb

-14 3^-14 2²³ 8388608 / 4782969 C^bb

-15 3^-15 2²⁴ 16777216 / 14348907 F^bb

-16 3^-16 2²⁶ 67108864 / 43046721 B^bbb

-17 3^-17 2²⁷ 134217728 / 129140163 E^bbb

-18 3^-18 2²⁹ 536870912 / 387420489 A^bbb

-19 3^-19 2³¹ 2147483648 / 1162261467 D^bbb

-20 3^-20 2³² 4294967296 / 3486784401 G^bbb

**Table 1**: Pythagorean fractions
Index	Three	Two	Fractional Value	Note Name
20	3²⁰	2^-31	3486784401 / 2147483648	F^###
19	3¹⁹	2^-30	1162261467 / 1073741824	B^##
18	3¹⁸	2^-28	387420489 / 268435456	E^##
17	3¹⁷	2^-26	129140163 / 67108864	A^##
16	3¹⁶	2^-25	43046721 / 33554432	D^##
15	3¹⁵	2^-23	14348907 / 8388608	G^##
14	3¹⁴	2^-22	4782969 / 4194304	C^##
13	3¹³	2^-20	1594323 / 1048576	F^##
12	3¹²	2^-19	531441 / 524288	B^#
11	3¹¹	2^-17	177147 / 131072	E^#
10	3¹⁰	2^-15	59049 / 32768	A^#
9	3⁹	2^-14	19683 / 16384	D^#
8	3⁸	2^-12	6561 / 4096	G^#
7	3⁷	2^-11	2187 / 2048	C^#
6	3⁶	2^-9	729 / 512	F^#
5	3⁵	2^-7	243 / 128	B
4	3⁴	2^-6	81 / 64	E
3	3³	2^-4	27 / 16	A
2	3²	2^-3	9 / 8	D
1	3¹	2^-1	3 / 2	G
0	3⁰	2⁰	1	C
-1	3^-1	2²	4 / 3	F
-2	3^-2	2⁴	16 / 9	B^b
-3	3^-3	2⁵	32 / 27	E^b
-4	3^-4	2⁷	128 / 81	A^b
-5	3^-5	2⁸	256 / 243	D^b
-6	3^-6	2¹⁰	1024 / 729	G^b
-7	3^-7	2¹²	4096 / 2187	C^b
-8	3^-8	2¹³	8192 / 6561	F^b
-9	3^-9	2¹⁵	32768 / 19683	B^bb
-10	3^-10	2¹⁶	65536 / 59049	E^bb
-11	3^-11	2¹⁸	262144 / 177147	A^bb
-12	3^-12	2²⁰	1048576 / 531441	D^bb
-13	3^-13	2²¹	2097152 / 1594323	G^bb
-14	3^-14	2²³	8388608 / 4782969	C^bb
-15	3^-15	2²⁴	16777216 / 14348907	F^bb
-16	3^-16	2²⁶	67108864 / 43046721	B^bbb
-17	3^-17	2²⁷	134217728 / 129140163	E^bbb
-18	3^-18	2²⁹	536870912 / 387420489	A^bbb
-19	3^-19	2³¹	2147483648 / 1162261467	D^bbb
-20	3^-20	2³²	4294967296 / 3486784401	G^bbb

A good way to draw circle of 5ths-type scales

Here is an illustrative diagram of how the Pythagorean sequence of notes is generated and rescaled into a single octave. Note that the vertical axis is log scaled. The straight red line has slope log(3) and it represents ascending by powers of 3. The jagged blue line represents the appropriate power of 2 to rescale the power of 3. This type of diagram will prove useful for us for showing many things later on.

log( 3ⁿ 2^κ(n) )	=	n log(3) + κ(n) log(2)
	=	Q(n) - R(n)

where R(n) := -κ(n) log(2)

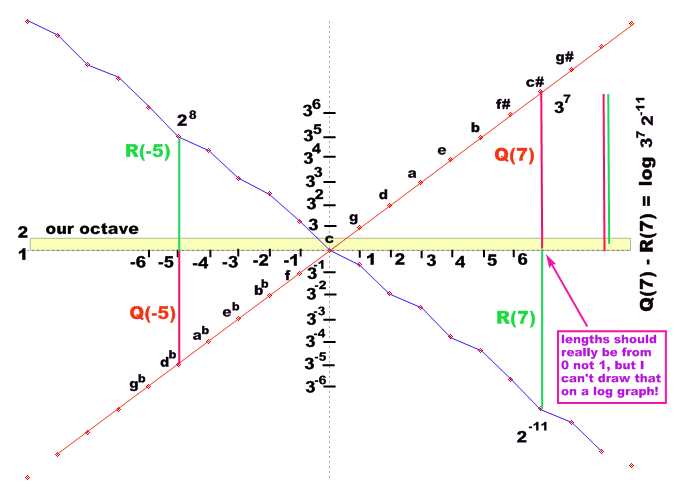
In Figure 2, this is illustrated for n = 7; the length of segment Q(7) minus R(7) shows the position inside the horizontal strip for the note. If any two note values would coincide, then we could stop the infinite sequence of generating new notes. (More on this in the next section).

Fig. 2

The closing condition

It isn't practical to have an infinite number of notes, so we have to cut off the progression. We have to stop at some point on the Sharps branch and at some point on the Flats branch, and we have to join the branches together. Cutting off the progression of notes arbitrarily produces wolf intervals (which we shall discuss in detail later) What are good closing points? Ideally, two notes would be equal and we wouldn't have an infinite progression. Let us show that this can never happen. Suppose, for n≠m, two notes would be equal:
3ⁿ 2^κ(n) = 3^m 2^κ(m)
then
3^{(n - m)} = 2^{(κ(m)- κ(n) )}
But this is impossible, because the left hand side is prime factored, and it contains only 3s while the right is prime factored into only 2s, so they can never be equal! Thus the pure 3rd harmonic sequence never repeats itself, it is infinite (although if you generate it far enough, the numbers get arbitrarily close) Let us examine some good cutoff points:

Observe that 3 = 2^α for α = log(3)/log(2)
then 3^m = 2^{α m}. Let p be the nearest whole number to αm. Then we need only use a calculator to get the values for αm for each positive integer m; the ones that are close to integers are good oportunities for the cycle of 5ths to close:

Table 2: Some good closing points for the pure 3rd harmonic sequence
m (power of 3) value α m p (power of 2)

12 19.0195 19

41 64.98 65

53 84.003 84

306 484.9985 485

**Table 2**: Some good closing points for the pure 3rd harmonic sequence
m (power of 3)	value α m	p (power of 2)
12	19.0195	19
41	64.98	65
53	84.003	84
306	484.9985	485

Now let's compare this very simple method with a brute force calculation using a Perl script genPythag.pl

(Almost) Symmetric generation of notes by the script

Starting at n = 0 for c, the script generates the next note on the sharps branch (namely g for n=1 ) and checks it against all previous notes generated to see which one it is closest to in pitch. Then it generates the next note on the flats branch (namely f for n = -1 ) and checks this note against the previous collection [See Fig 1]. It keeps going in this manner until it reaches the maximum number of iterations that was on the command line when the script was invoked. Here is the syntax to run the script:

perl -w genPythag.pl 30 CLOSING > table.html

and look at the output file table.html with your web browser. The first argument, the number 30, was the maximum number of iterations to do; it will calculate 30 pairs of notes, one on the sharps branch and one on the flats. The second argument, the string CLOSING, tells the script which action to execute; there are a number of posibile actions, and they have all been used at various points in the development of this web page.

Table 3: closing points with pure 3rd Harmonic
Count of notes
generated m =
notes in scale New note
name New note
value Best match
value Best match
name Distance in cents
6 5 A 3³ 2^-4 3^-2 2⁴ B^b 90.2249956730629
13 12 G^b 3^-6 2¹⁰ 3⁶ 2^-9 F^# 23.4600103846492
42 41 C^### 3²¹ 2^-33 3^-20 2³² G^bbb 19.844964519116
54 53 F^4# 3²⁷ 2^-42 3^-26 2⁴² D^4b 3.61504586553314
307 306 G^22b 3^-153 2²⁴³ 3¹⁵³ 2^-242 F^22# 1.76973519144986

**Table 3**: closing points with pure 3rd Harmonic
Count of notes generated	m = notes in scale	New note name	New note value	Best match value	Best match name	Distance in cents
6	5	A	3³ 2^-4	3^-2 2⁴	B^b	90.2249956730629
13	12	G^b	3^-6 2¹⁰	3⁶ 2^-9	F^#	23.4600103846492
42	41	C^###	3²¹ 2^-33	3^-20 2³²	G^bbb	19.844964519116
54	53	F^4#	3²⁷ 2^-42	3^-26 2⁴²	D^4b	3.61504586553314
307	306	G^22b	3^-153 2²⁴³	3¹⁵³ 2^-242	F^22#	1.76973519144986

So what do we see comparing Table 3 with Table 2?
Observe that if we generate 13 notes in the symmetric manner described above, then g^b almost coincides with f^#. This is the m = 12 row in Table 2. Every additional new note generated is that exact distance from its enharmonic equivalent until we get to the count of 42; (that is m = 41). Finally when we have generated 307 notes, we note that the -153rd one ( g with 22 flats ) comes extremely close to the +153rd one ( f with 22 sharps ). And you can keep on going, if you are so inclined...

An "Amazing Coincidence"...

Let us look at Table 3 in more detail. In particular, lets compute all the intermediate values. From looking at the generating function P_y(n) = 3ⁿ · 2^κ(n) I would naively think that the best closing distance would vary quite a bit from note to note as they are generated, but in fact the distance is always the same, until points when it decreases in steps! This is apparent from looking at the following table (where there is some variation in the last decimal place, but that is just due to numerical round off errors).

Table 4: More detail of closing behavior
Count New note name new note value best match value best match Name Distance in cents
4 D 3² 2^-3 3⁰ 2⁰ C 203.910001730775
5 B^b 3^-2 2⁴ 3⁰ 2⁰ C 203.910001730775
6 A 3³ 2^-4 3^-2 2⁴ B^b 90.2249956730629
7 E^b 3^-3 2⁵ 3² 2^-3 D 90.2249956730627
8 E 3⁴ 2^-6 3^-1 2² F 90.2249956730629
9 A^b 3^-4 2⁷ 3¹ 2^-1 G 90.2249956730627
10 B 3⁵ 2^-7 3⁰ 2⁰ C 90.2249956730629
11 D^b 3^-5 2⁸ 3⁰ 2⁰ C 90.2249956730631
12 F^# 3⁶ 2^-9 3¹ 2^-1 G 90.2249956730629
13 G^b 3^-6 2¹⁰ 3⁶ 2^-9 F^# 23.4600103846492
14 C^# 3⁷ 2^-11 3^-5 2⁸ D^b 23.460010384649
15 C^b 3^-7 2¹² 3⁵ 2^-7 B 23.4600103846492
16 G^# 3⁸ 2^-12 3^-4 2⁷ A^b 23.460010384649
17 F^b 3^-8 2¹³ 3⁴ 2^-6 E 23.460010384649
18 D^# 3⁹ 2^-14 3^-3 2⁵ E^b 23.460010384649
19 B^bb 3^-9 2¹⁵ 3³ 2^-4 A 23.4600103846492
20 A^# 3¹⁰ 2^-15 3^-2 2⁴ B^b 23.460010384649
21 E^bb 3^-10 2¹⁶ 3² 2^-3 D 23.4600103846492
22 E^# 3¹¹ 2^-17 3^-1 2² F 23.460010384649
23 A^bb 3^-11 2¹⁸ 3¹ 2^-1 G 23.460010384649
24 B^# 3¹² 2^-19 3⁰ 2⁰ C 23.460010384649
25 D^bb 3^-12 2²⁰ 3⁰ 2⁰ C 23.460010384649
26 F^## 3¹³ 2^-20 3¹ 2^-1 G 23.460010384649
27 G^bb 3^-13 2²¹ 3^-1 2² F 23.460010384649
28 C^## 3¹⁴ 2^-22 3² 2^-3 D 23.460010384649
29 C^bb 3^-14 2²³ 3^-2 2⁴ B^b 23.460010384649
30 G^## 3¹⁵ 2^-23 3³ 2^-4 A 23.460010384649
31 F^bb 3^-15 2²⁴ 3^-3 2⁵ E^b 23.460010384649
32 D^## 3¹⁶ 2^-25 3⁴ 2^-6 E 23.460010384649
33 B^bbb 3^-16 2²⁶ 3^-4 2⁷ A^b 23.460010384649
34 A^## 3¹⁷ 2^-26 3⁵ 2^-7 B 23.460010384649
35 E^bbb 3^-17 2²⁷ 3^-5 2⁸ D^b 23.4600103846492
36 E^## 3¹⁸ 2^-28 3⁶ 2^-9 F^# 23.460010384649
37 A^bbb 3^-18 2²⁹ 3^-6 2¹⁰ G^b 23.460010384649
38 B^## 3¹⁹ 2^-30 3⁷ 2^-11 C^# 23.460010384649
39 D^bbb 3^-19 2³¹ 3^-7 2¹² C^b 23.460010384649
40 F^### 3²⁰ 2^-31 3⁸ 2^-12 G^# 23.460010384649
41 G^bbb 3^-20 2³² 3^-8 2¹³ F^b 23.460010384649
42 C^### 3²¹ 2^-33 3^-20 2³² G^bbb 19.844964519116
43 C^bbb 3^-21 2³⁴ 3²⁰ 2^-31 F^### 19.8449645191159
44 G^### 3²² 2^-34 3^-19 2³¹ D^bbb 19.8449645191158
45 F^bbb 3^-22 2³⁵ 3¹⁹ 2^-30 B^## 19.8449645191159
46 D^### 3²³ 2^-36 3^-18 2²⁹ A^bbb 19.8449645191158
47 B^4b 3^-23 2³⁷ 3¹⁸ 2^-28 E^## 19.8449645191159
48 A^### 3²⁴ 2^-38 3^-17 2²⁷ E^bbb 19.844964519116
49 E^4b 3^-24 2³⁹ 3¹⁷ 2^-26 A^## 19.8449645191159
50 E^### 3²⁵ 2^-39 3^-16 2²⁶ B^bbb 19.8449645191158
51 A^4b 3^-25 2⁴⁰ 3¹⁶ 2^-25 D^## 19.8449645191159
52 B^### 3²⁶ 2^-41 3^-15 2²⁴ F^bb 19.8449645191158
53 D^4b 3^-26 2⁴² 3¹⁵ 2^-23 G^## 19.8449645191159
54 F^4# 3²⁷ 2^-42 3^-26 2⁴² D^4b 3.61504586553314
55 G^4b 3^-27 2⁴³ 3²⁶ 2^-41 B^### 3.61504586553324
56 C^4# 3²⁸ 2^-44 3^-25 2⁴⁰ A^4b 3.61504586553314
57 C^4b 3^-28 2⁴⁵ 3²⁵ 2^-39 E^### 3.61504586553324

**Table 4:** More detail of closing behavior
Count	New note name	new note value	best match value	best match Name	Distance in cents
4	D	3² 2^-3	3⁰ 2⁰	C	203.910001730775
5	B^b	3^-2 2⁴	3⁰ 2⁰	C	203.910001730775
6	A	3³ 2^-4	3^-2 2⁴	B^b	90.2249956730629
7	E^b	3^-3 2⁵	3² 2^-3	D	90.2249956730627
8	E	3⁴ 2^-6	3^-1 2²	F	90.2249956730629
9	A^b	3^-4 2⁷	3¹ 2^-1	G	90.2249956730627
10	B	3⁵ 2^-7	3⁰ 2⁰	C	90.2249956730629
11	D^b	3^-5 2⁸	3⁰ 2⁰	C	90.2249956730631
12	F^#	3⁶ 2^-9	3¹ 2^-1	G	90.2249956730629
13	G^b	3^-6 2¹⁰	3⁶ 2^-9	F^#	23.4600103846492
14	C^#	3⁷ 2^-11	3^-5 2⁸	D^b	23.460010384649
15	C^b	3^-7 2¹²	3⁵ 2^-7	B	23.4600103846492
16	G^#	3⁸ 2^-12	3^-4 2⁷	A^b	23.460010384649
17	F^b	3^-8 2¹³	3⁴ 2^-6	E	23.460010384649
18	D^#	3⁹ 2^-14	3^-3 2⁵	E^b	23.460010384649
19	B^bb	3^-9 2¹⁵	3³ 2^-4	A	23.4600103846492
20	A^#	3¹⁰ 2^-15	3^-2 2⁴	B^b	23.460010384649
21	E^bb	3^-10 2¹⁶	3² 2^-3	D	23.4600103846492
22	E^#	3¹¹ 2^-17	3^-1 2²	F	23.460010384649
23	A^bb	3^-11 2¹⁸	3¹ 2^-1	G	23.460010384649
24	B^#	3¹² 2^-19	3⁰ 2⁰	C	23.460010384649
25	D^bb	3^-12 2²⁰	3⁰ 2⁰	C	23.460010384649
26	F^##	3¹³ 2^-20	3¹ 2^-1	G	23.460010384649
27	G^bb	3^-13 2²¹	3^-1 2²	F	23.460010384649
28	C^##	3¹⁴ 2^-22	3² 2^-3	D	23.460010384649
29	C^bb	3^-14 2²³	3^-2 2⁴	B^b	23.460010384649
30	G^##	3¹⁵ 2^-23	3³ 2^-4	A	23.460010384649
31	F^bb	3^-15 2²⁴	3^-3 2⁵	E^b	23.460010384649
32	D^##	3¹⁶ 2^-25	3⁴ 2^-6	E	23.460010384649
33	B^bbb	3^-16 2²⁶	3^-4 2⁷	A^b	23.460010384649
34	A^##	3¹⁷ 2^-26	3⁵ 2^-7	B	23.460010384649
35	E^bbb	3^-17 2²⁷	3^-5 2⁸	D^b	23.4600103846492
36	E^##	3¹⁸ 2^-28	3⁶ 2^-9	F^#	23.460010384649
37	A^bbb	3^-18 2²⁹	3^-6 2¹⁰	G^b	23.460010384649
38	B^##	3¹⁹ 2^-30	3⁷ 2^-11	C^#	23.460010384649
39	D^bbb	3^-19 2³¹	3^-7 2¹²	C^b	23.460010384649
40	F^###	3²⁰ 2^-31	3⁸ 2^-12	G^#	23.460010384649
41	G^bbb	3^-20 2³²	3^-8 2¹³	F^b	23.460010384649
42	C^###	3²¹ 2^-33	3^-20 2³²	G^bbb	19.844964519116
43	C^bbb	3^-21 2³⁴	3²⁰ 2^-31	F^###	19.8449645191159
44	G^###	3²² 2^-34	3^-19 2³¹	D^bbb	19.8449645191158
45	F^bbb	3^-22 2³⁵	3¹⁹ 2^-30	B^##	19.8449645191159
46	D^###	3²³ 2^-36	3^-18 2²⁹	A^bbb	19.8449645191158
47	B^4b	3^-23 2³⁷	3¹⁸ 2^-28	E^##	19.8449645191159
48	A^###	3²⁴ 2^-38	3^-17 2²⁷	E^bbb	19.844964519116
49	E^4b	3^-24 2³⁹	3¹⁷ 2^-26	A^##	19.8449645191159
50	E^###	3²⁵ 2^-39	3^-16 2²⁶	B^bbb	19.8449645191158
51	A^4b	3^-25 2⁴⁰	3¹⁶ 2^-25	D^##	19.8449645191159
52	B^###	3²⁶ 2^-41	3^-15 2²⁴	F^bb	19.8449645191158
53	D^4b	3^-26 2⁴²	3¹⁵ 2^-23	G^##	19.8449645191159
54	F^4#	3²⁷ 2^-42	3^-26 2⁴²	D^4b	3.61504586553314
55	G^4b	3^-27 2⁴³	3²⁶ 2^-41	B^###	3.61504586553324
56	C^4#	3²⁸ 2^-44	3^-25 2⁴⁰	A^4b	3.61504586553314
57	C^4b	3^-28 2⁴⁵	3²⁵ 2^-39	E^###	3.61504586553324

...And Its Resolution

The right picture clears everything up, and in discussions of temperament, the right picture is usually log scaled. Let us draw a picture where the octave rescaling function κ plays no role. The pure 3rd harmonic sequence is generated by 3ⁿ, and when the y-axis is log scaled, the points y(n) = n log(3) form a straight line. [This also has relevance to α-comma meantone, which we discuss next, and indeed any generated sequence of notes of the form θⁿ].

Fig. 3

The diagram shows a note high up on the line matching with another note m positions in the flats direction behind it. Δ_p represents all the vertical distance that can be cancelled out by octave equivalence; the leftover portion δ represents the pitch difference between the two notes when they are put into the same octave.

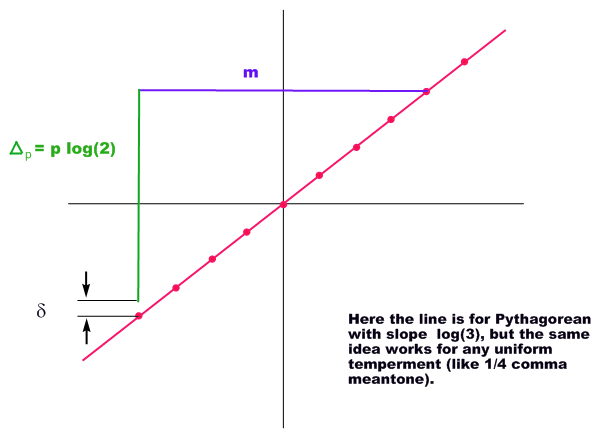
If we have a straight diagonal line like this, then obviously we can slide the right angle "elbow" piece up and down the line and the relationship between m, Δ_p and δ still holds. Thus:
δ = distance( f^#, g^b ) = distance( c^#, d^b ) = ... = distance( b^##, c^# ) ...

The determining factor is the range of allowable values for the length m; for 1 ≤ m ≤ 40 the best we can do is m = 12 then p = 19 and δ = 23.46001038...¢ (the Pythagorean comma ρ) but allow m to reach as high as 53 and then p = 485 really makes δ small!

Go to Next Section: Acoustic Landmarks

Perl source code genPythag.pl to generate these tables.

Return to root of my Music Theory section
Return to Home Page
Send me email: jjensen14@hotmail.com Advisory: messages with keywords typical of spam in the subject line (including "!" as in "Get out of debt!") get automatically discarded before I see them.