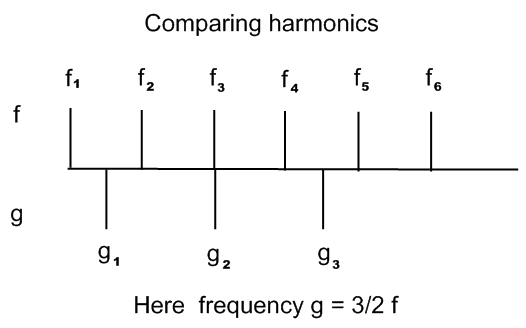
F = ( f1, f2, f3, f4, f5, f6 ) where fi := i * f1
and tone 2 by G = ( g1, g2, g3, g4, g5, g6 ) , with corresponding arrays for the amplitudes of each individual harmonic.
The Dissonance Curve and Applet
2 tones of moderate loudness, sounded simultaneously, are said to be dissonant if the result is unpleasant to listen to, and consonant if they blend well together, and are pleasing to listen to. The explanation of what causes dissonance (specifically sensory dissonance) is the beats produced by a harmonic of the first tone, when it is near, but does not coincide in frequency with a harmonic of the second. However, if the beats are very slow or extremely fast, the effect is not so unpleasant. There is an interesting discussion of this and more in [Pierce 1983 p.76], including the human ear, and the unpleasantness of dissonance resulting from 2 different sounds transmitting along the same nerve fibres. There is also the confounding effect of musically trained individuals being sensitive to what intervals they expect to be consonant or dissonant, based on past experience. This is omitted from the mathematical model below.
Let us now consider tones with no harmonics higher than the first, i.e. pure sine waves. Fix tone 1 at frequency f, and denote the frequency of the other tone by g. As g varies upward from f, there is a region of roughness or critical bandwidth where there is dissonance; this dissonance dies down as g continues to increase. The length of the critical bandwidth depends on the base frequency f, and Pierce gives the rule of thumb that it extends to about the minor 3rd, that is 6/5 f. The strength of the dissonance sensation is a smooth bump function, reaching a single maximum at about 1/4 of the length of the critical bandwidth.

What we now have is a weight function for the amount of dissonance between 2 pure
tones. [Sethares 1997] gives an excellent discussion dissonance curves, the
experiments of Plomp in the 1960s, and provides optimal curve fitted parameters
from the data of Plomp and Levelt, which we shall use. [Benson 2002] also provides
an informative discussion.
We can now give a mathematical expression for the dissonance weight function as:
d( f, g, Af, Ag ) = Af Ag
[e
-0.84Q
-
e
-1.38Q
]
where Q =
( g - f)
--------------
0.021 f + 19
where Af is the amplitude of f, Ag is the amplitude
of g, and g >= f.
Then for standard musical tones with harmonics, we can compute the total dissonance
by summing the dissonance of each pair of harmonics. We
represent the significant harmonics of tone 1 by the array
F = ( f1, f2, f3, f4, f5, f6 ) where fi := i * f1
and tone 2
by G = ( g1, g2, g3, g4, g5, g6 ) ,
with corresponding arrays for the amplitudes of each individual harmonic.

We then loop over each element of array F, and for each element of F we loop over array G, summing up the result of plugging fi and gj into d( f, g, Af, Ag), with the warning that f is always the minimum term of {fi, gj}, and g is always the maximum. The following applet draws the curve as g1 varies over the octave of f1.
Dissonance Curve AppletPlucked: (1.0 0.8 0.6 0.3 0.1 0.03)
Soft hammer: (1.0 1.9 1.1 0.2 0.0 0.05)
Medium hammer: (1.0 2.9 3.6 2.6 1.1 0.2 )
Hard hammer: (1.0 3.2 5.0 5.0 3.2 1.0 )
Discussion of Results for scales
The above applet's diagram tells us how well the frequencies blend with the base frequency, which we always call C. The reader should systematically experiment with increasing base frequencies and harder hammers ( the harder the hammer, the more prominence of the upper harmonics). A number of interesting phenomena emerge, and we shall discuss some of them, while wondering which are artifacts of Plomp's model, or Sethares' parameters, or the author's own implementation.
Some general observations (by no means all):
Let us take as our baseline middle C = 264Hz and the Medium hammer. Any scale we
derive in the primary octave would just be transposed to upper and lower octaves.
Recall that the Just Intonation C scale has frequency ratios
C major: (C-D-E-F-G-A-B) = [ 1 9/8 5/4 4/3 3/2 5/3 15/8 ]
C minor: (C-D-Eb-F-G-Ab-Bb) = [ 1 9/8 6/5 4/3 3/2 8/5 9/5 ]
We would like to show that these choices are optimal in some fundamental sense.
This will lead us into functional harmony, which is not well understood by the author,
but we'll go as far as we can. We defined the C major scale from the notes of
the triad chords C, F, G based on harmonics.
Here we ask what that means in terms of the amount of dissonance.
The C major triad is certainly very consonant with C, therefore it is in the
scale. The F chord is then a great choice because its gets both the other
consonance heavyweights F and A. Why not use A major if A is so good? The
problem is the almost maximum dissonance around C# ( and no leading tone
property to C).
How do we justify the G chord being part of the scale?
G is excellent with C alone, but B and D are terrible, they do not even appear
as local minima; 3 octaves up at 2112Hz, we get a deep but wide minima near D
and a bit higher than B-flat ( but never B!). Perhaps this very weakness can
be construed as a strength, though. The notes of the G chord serve two functions:
Idea: It would be interesting to see if one could construct a mathematical function to indicate what chord ( if any) a given chord should resolve to, perhaps a "dissonance metric" to give the shortest path to a satisfactorily consonant chord. Also, by plotting the dissonance value of chords, could one study classical music in a dynamical systems approach as trajectories winding around on dissonance surfaces, and interacting with minima, like a particle in a potential energy well?
We may reasonably postulate the following as another musical axiom, and justify it
by the lack of general acceptance of 20th century atonal music:
Resolution Axiom: A critically important function of harmony in music
is the "tension" of dissonant harmony resolving into the "relaxation" of consonance,
usually the tonic chord.
For the minor scales, we again have the dissonance minima at C, F, G and A; we form the minor triads for C,F and G ( Am is already in C major ). With the Fm we lose the strong consonance of A with C and instead have Ab. Historically, people had trouble accepting a minor chord ending a composition, but it sounds perfectly acceptable today. This fact could play havoc with creating the above mentioned chord resolution function.
return to main document:Contents